“expand out” the multiplication first is a convention that the mathematics community agreed on, not a fact that can be proven

Order of operations proof - simple version

Thanks for the effort!

You’re welcome.

Just proves, never too late to learn :-)

I would have got 1 by doing 2(2+2) = 8 first. Not because of bracket but because of “implied multiplication.”

Yeah, right answer but wrong reason. There’s no such thing as implicit multiplication.

What I am learning here: 8÷2(2+2) is not same as 8÷2×(2+2)

Correct, and that’s because of Terms - 8÷2(2+2) is 2 terms, with the (2+2) in the denominator, but 8÷2×(2+2) is 3 terms, with the (2+2) in the numerator… hence why people get the wrong answer when they add an extra multiply in.

number next bracket is not the same as normal multiplication in rule book

Right, because it’s not “multiplication” at all (only applies literally to multiplication signs), it’s a coefficient of a bracketed term, which means we have to apply The Distributive Law as part of solving Brackets.

÷ & × have right of way rule with whoever is left most wins

Yeah, the actual rule is Left associativity, and going left to right is the easy way to obey that.

multiple always happens first. But apparently it’s what’s left side first

Multiplication and division are equal precedence (and done left to right) if that’s what you’re talking about, but the issue is that a(b+c) isn’t “multiplication” at all, it’s a bracketed term with a coefficient which is therefore subject to The Distributive Law, and is solved as part of solving Brackets, which is always first. Multiplication refers literally to multiplication signs, of which there are none in the original question. A Term is a product, which is the result of a multiplication, not something which is to be multiplied.

If a=2 and b=3, then…

axb=2x3 - 2 terms

ab=6 - 1 term

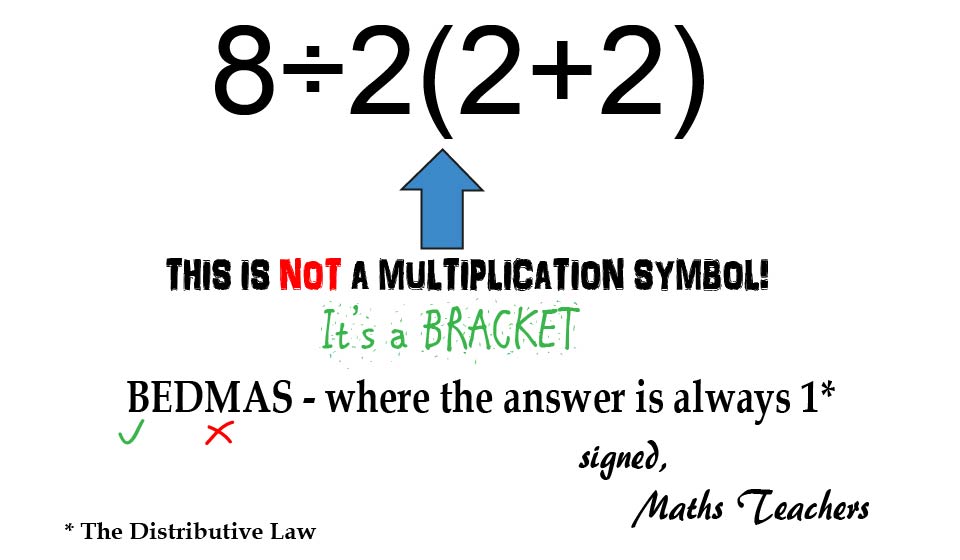
Ok, that’s a start. In your simple example they are all equal, but they aren’t all the same.

yn+y - 2 terms

y(n+1) - 1 term

y×(n +1) - 2 terms

To see the difference, now precede it with a division, like in the original question…

1÷yn+y=(1/yn)+y

1÷y(n+1)=1/(yn+y)

1÷y×(n +1)=(n +1)/y

Note that in the last one, compared to the second one, the (n+1) is now in the numerator instead of in the denominator. Welcome to why having the (2+2) in the numerator gives the wrong answer.

The y(n+1) is same as yn + y

No, it’s the same as (yn+y). You can’t remove brackets unless there is only 1 term left inside.

if you removed the “6÷” part. It’s

…The Distributive Law.

It doesn’t make sense in BODMAS either. Expanding Brackets has precedence of… Brackets, not “multiplication” - “Multiplication” refers literally to multiplication signs, of which there are none in this question.

Well thanks to you too for a proper conversation. :-) There’s a lot of people here wanting to pull out their pitchforks over the smallest thing.

e.g. you made a comment about teaching the “scientific” method to kids, and I can tell you as a teacher that we already do (but the OP never looked at any Maths textbooks, nor asked any Maths teachers) :-)

Yeah, I thought maybe you meant that, but I wasn’t sure, and in any case I wanted to make clear it’s totally worthless to use as a source for anything else (for the reasons I mentioned). :-)

That’s cool. I’m not sure what you mean about not using it as a source though, because that was also my point! If you want sources for how this should actually be done (and what actually is taught at school), then see my thread - contains actual textbook references (where there’s a screenshot of a textbook, the place it’s come from is in the top-left of the screenshot), actual historical documents (Lennes and Cajori), worked examples, proofs, etc. You said you believe in “strong juxtaposition”, so we’re kinda in agreement - I’m just pointing out that the actual rules are Terms and The Distributive Law (i.e. 2 different rules have been lumped together as one under the “strong juxtaposition” banner), neither of which is discussed anywhere in the blog (and when I, and others, have pointed this out, the OP has ignored us and downvoted our comments). I also made 5 fact check posts rebutting the false/misleading claims made in the blog - just sort the comments here by “new” and you’ll see them (no prizes for guessing who downvoted them).

In other words, I wasn’t saying “don’t pay attention to any blog posts” (which I think is what you thought I meant?), I was saying “don’t pay attention to this blog post” (for multiple reasons that I’ve posted in many places in here).

Not sure how you came up with that conclusion. I never said anything about it being “just a blog post”.

You said…

I don’t understand how the author of the post lands on “there is no good or bad way, they are all valid”

And I’m pointing out he arrived at that by ignoring what’s taught in high school, which is where it’s taught (not in academia). It’s like saying “It’s ambiguous if there’s such a thing as rain” if you present weather evidence which has omitted every single rainy day that has happened. i.e. cherry-picking. Every single blog which says it’s ambiguous has done the exact same thing. You can find what actually is taught in high school here

Check a high school Maths textbook - even easier!

It’s what is actually taught in high school, so there are those who remember and those who don’t.

You are correct with your definition - Terms are separated by operators and joined by grouping symbols - and it’s consequently not ambiguous at all (using so-called “weak juxtaposition” breaks that rule).

enforce writing math without ambiguity

It already is written without ambiguity.

were taught in third grade

This is actually taught in Year 7 - the people who only remember the 3rd Grade version of the rules are the ones getting it wrong.

There isn’t ambiguity to begin with - just people who have forgotten the rules of Maths.

I wanted to compile a list of points that show as clear as humanity possible that there is no consensus here, even amongst experts

And I wrote a bunch of fact checks pointing out there is consensus amongst the actual experts - high school Maths teachers and textbook authors, the 2 groups who you completely ignored in your blog post.

What’s especially wild to me is that even the position of “it’s ambiguous” gets almost as much pushback as trying to argue that one of them is universally correct.

That’s because following the rules of Maths is universally correct.

arguing vehemently that implicit multiplication having precedence was correct and to do otherwise was wrong, full stop

He was using the wrong words, but he was correct - the actual rules are The Distributive Law and Terms (“implicit multiplication” is a rule made up by those who have forgotten these 2 rules).